प्रकाश- परावर्तन तथा अपवर्तन
प्रकाश क्या है?
प्रकाश वह ऊर्जा है जिसके द्वारा हम वस्तुओं को देख सकते हैं।
प्रकाश के गुण
- प्रकाश सरल (सीधी) रेखाओं में गमन करता है।
- प्रकाश विद्युत चुंबकीय तरंग है इसलिए इसे संचारण के लिए माध्यम की आवश्यक्ता नहीं पड़ती।
- प्रकाश अपारदर्शीय वस्तुओं की तीक्ष्ण छाया बनाता है।
- प्रकाश की चाल निर्वात में सबसे अधिक है (3 × 10^8 m/s)
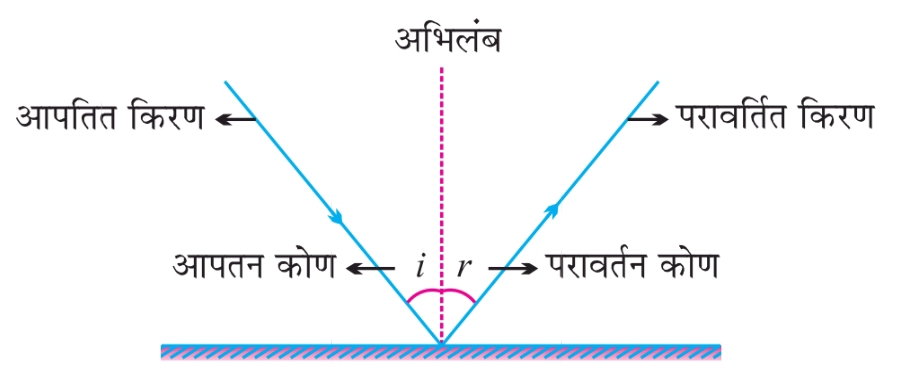
प्रकाश के परावर्तन के नियम
- आपतन कोण, परावर्तन कोण के बराबर होता है।
- आपतित किरण, दर्पण के आपतन बिंदु पर अभिलंब होती है और परावर्तित किरण, आपतन बिंदु पर दर्पण की सतह के समांतर एक ही तल में होती हैं।
प्रतिबिंब: प्रतिबिंब उस बिंदु पर बनता है जहाँ दो या दो से अधिक परावर्तित किरणें एक दूसरे को प्रतिच्छेदित करती हैं, या ऐसा प्रतीत होता है कि वे प्रतिच्छेदित हो रही हैं।
|
वास्तविक प्रतिबिंब
|
आभासी प्रतिबिंब
|
|
(i) यह तब बनता है जब प्रकाश की किरणें वास्तव में प्रतिच्छेदित होती हैं।
|
(i) यह तब बनता है जब प्रकाश की किरणें प्रतिच्छेदित होती प्रतीत होती हैं।
|
|
(ii) इसे परदे पर प्राप्त कर सकते हैं।
|
(ii) इसे परदे पर प्राप्त नहीं कर सकते।
|
|
(iii) वास्तविक प्रतिबिंब उल्टा बनता है।
|
(iii) आभासी प्रतिबिंब सीधा बनता है।
|
समतल दर्पण द्वारा प्राप्त प्रतिबिंब
- आभासी एवं सीधा होता है।
- प्रतिबिंब का आकार वस्तु के आकार के बराबर होता है।
- प्रतिबिंब दर्पण के उतने पीछे बनता है जितनी वस्तु की दर्पण से दूरी होती है।
- प्रतिबिंब पार्श्व परिवर्तित होता है।
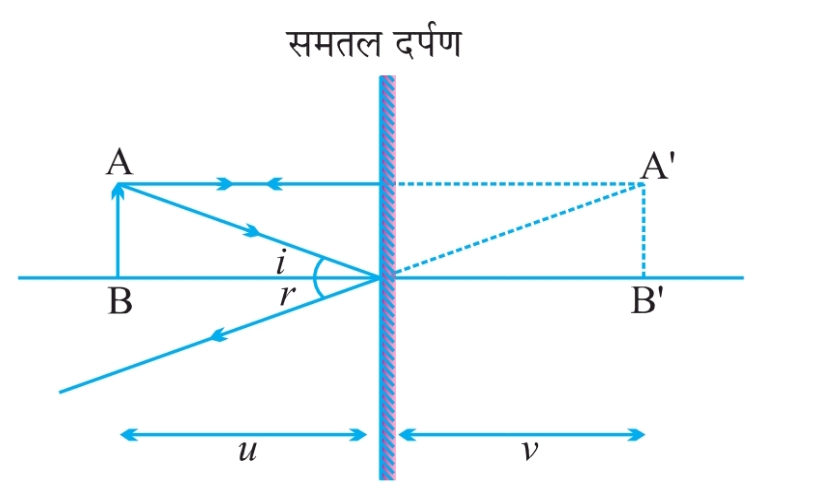
पार्श्व परिवर्तन
- इसमें वस्तु का दायां भाग बायां प्रतीत होता है और बायां भाग दायां।
गोलीय दर्पण
- गोलीय दर्पण का परावर्तक तल अंदर की ओर या बाहर की ओर वक्रित होता है
- गोलीय दर्पण जिसका परावर्तक पृष्ठ अंदर की ओर अर्थात् गोले के केंद्र की ओर वक्रित है वह अवतल दर्पण कहलाता है।
- गोलीय दर्पण जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित है, उत्तल दर्पण कहलाता है।
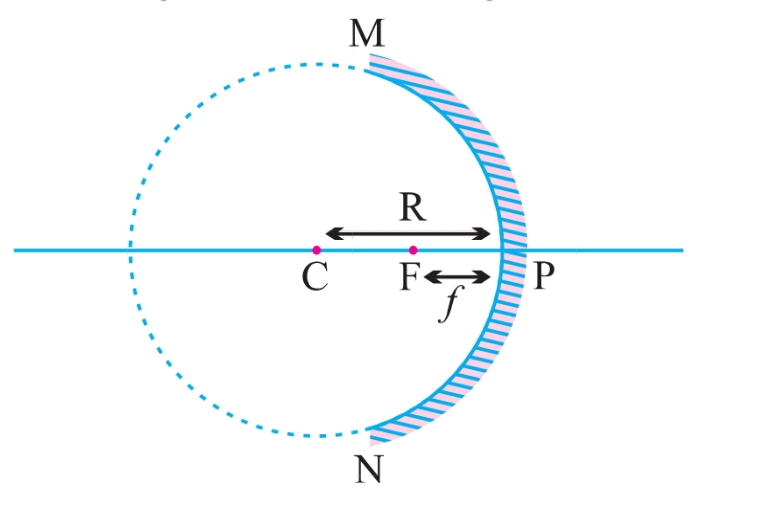
गोलीय दर्पण में प्रयुक्त महत्वपूर्ण शब्दावली
1. ध्रुव (Pole, P):
- दर्पण के परावर्तक पृष्ठ के केंद्र को ध्रुव कहते हैं।
2. मुख्य अक्ष (Principal Axis):
- दर्पण के ध्रुव और वक्रता केंद्र को जोड़ने वाली सीधी रेखा मुख्य अक्ष कहलाती है।
3. वक्रता केंद्र (Centre of Curvature, C):
- जिस गोले का भाग दर्पण होता है, उसका केंद्र वक्रता केंद्र कहलाता है।
4. वक्रता त्रिज्या (Radius of Curvature, R):
- वक्रता केंद्र से दर्पण के ध्रुव तक की दूरी वक्रता त्रिज्या कहलाती है।
5. द्वारक (Aperture, MN):
- दर्पण के परावर्तक पृष्ठ के व्यास को द्वारक कहते हैं।
6. मुख्य फोकस (Principal Focus, F):
- मुख्य अक्ष के समानांतर आने वाली किरणें परावर्तित होकर जिस बिंदु पर मिलती हैं या मिलती हुई प्रतीत होती हैं, उसे मुख्य फोकस कहते हैं।
7. फोकस दूरी (Focal Length, F):
- ध्रुव और मुख्य फोकस के बीच की दूरी फोकस दूरी कहलाती है।
महत्वपूर्ण तथ्य:
- छोटे द्वारक के दर्पणों के लिए, वक्रता त्रिज्या (R) फोकस दूरी (F) का दुगुना होता है
- यह संबंध R = 2F द्वारा दर्शाया जाता है।
अवतल दर्पण
अवतल दर्पण के किरण आरेख नियम
- मुख्य अक्ष के समांतर किरण परावर्तित होकर मुख्य फोकस से गुजरती है।

- मुख्य फोकस से गुजरने वाली किरण परावर्तित होकर मुख्य अक्ष के समांतर निकलती है।
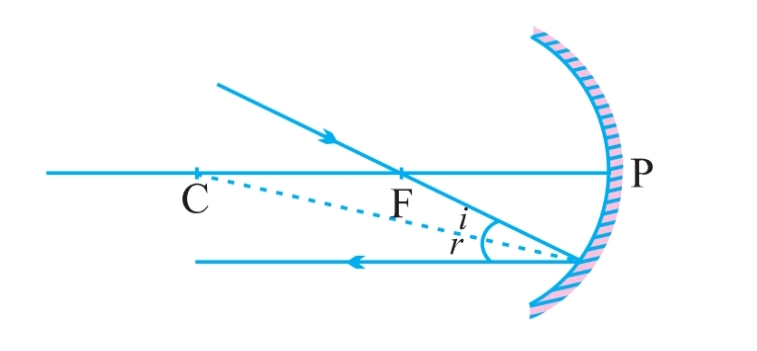
- वक्रता केंद्र से गुजरने वाली किरण वापस उसी दिशा में लौटती है क्योंकि यह अभिलंब की तरह कार्य करती है।
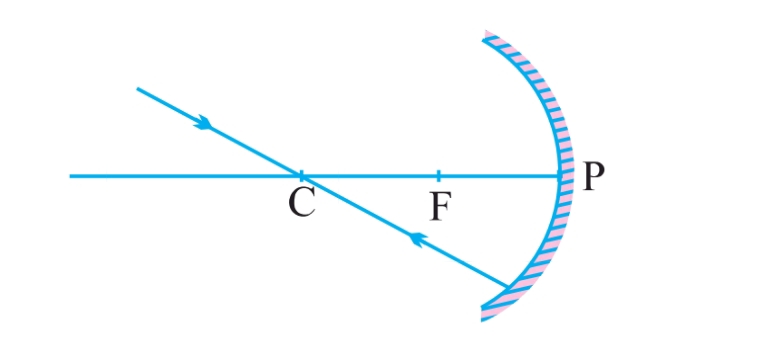
- मुख्य अक्ष से तिरछी किरणें तिरछी दिशा में ही परावर्तित होती हैं, और आपतन बिंदु पर मुख्य अक्ष के समान कोण बनाती हैं।

| बिंब की सिथति |
प्रतिबिंब की स्थिति |
प्रतिबिंब का आकार |
प्रतिबिंब की प्रकृति |
|
अनंत पर
|
अनंत दूरी पर |
अत्यंत छोटा |
वास्तविक और उल्टा |
| C से परे |
|
वास्तविक और छोटा |
वास्तविक और उल्टा |
| C पर |
C पर |
समान आकार |
वास्तविक और उल्टा |
| C तथा F के बीच |
C और F के बीच |
बड़ा |
वास्तविक और उल्टा |
| F पर |
F पर |
अत्यधिक बड़ा |
वास्तविक और उल्टा |
| P तथा F के बीच |
F से आगे |
बड़ा |
काल्पनिक और सीधा |
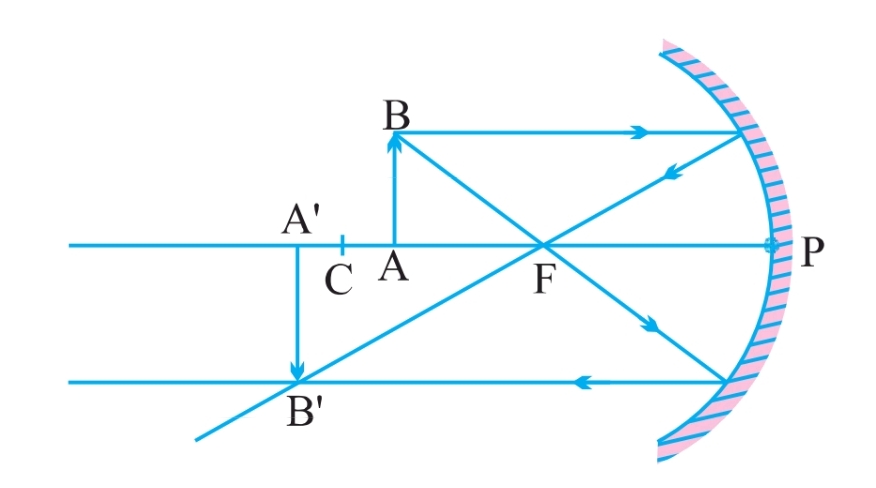
अवतल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब
(i) अनंत पर

(ii) C से परे

(iii) C पर

(iv) C तथा F के बीच
(v) F पर
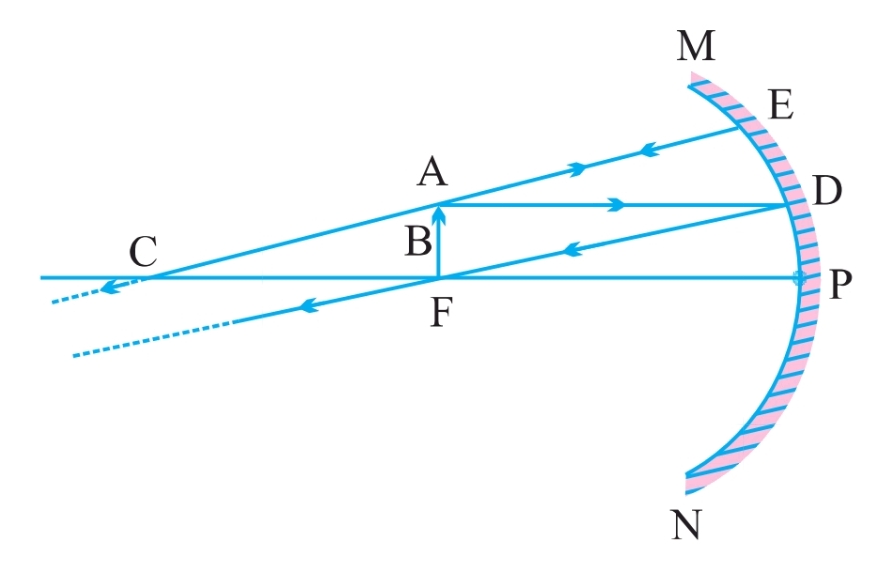
(vi) P तथा F के बीच
अवतल दर्पणों के उपयोग
- टॉर्च, सर्चलाइट और वाहनों की हैडलाइट में प्रकाश के समानांतर किरण पुंज के लिए अवतल दर्पण का उपयोग किया जाता है।
- दंत विशेषज्ञ दाँतों का बड़ा प्रतिबिंब देखने के लिए अवतल दर्पण का उपयोग करते हैं।
- शेविंग दर्पणों में चेहरे का बड़ा प्रतिबिंब देखने के लिए अवतल दर्पण का उपयोग होता है।
- सौर भट्टियों में सूर्य के प्रकाश को केंद्रित करने के लिए बड़े अवतल दर्पणों का उपयोग किया जाता है।
उत्तल दर्पण
मुख्य अक्ष के समांतर किरण (Parallel Ray):
- जब प्रकाश की किरण मुख्य अक्ष के समांतर दर्पण की ओर आती है, तो परावर्तित किरण मुख्य फोकस (F) से गुजरती है।

वक्रता केंद्र से गुजरने वाली किरण (Ray from Center of Curvature):
- यदि प्रकाश की किरण वक्रता केंद्र (C) से गुजरती है, तो यह परावर्तित होकर उसी दिशा में लौटती है, जैसे यह दर्पण के अभिलंब से आ रही हो।
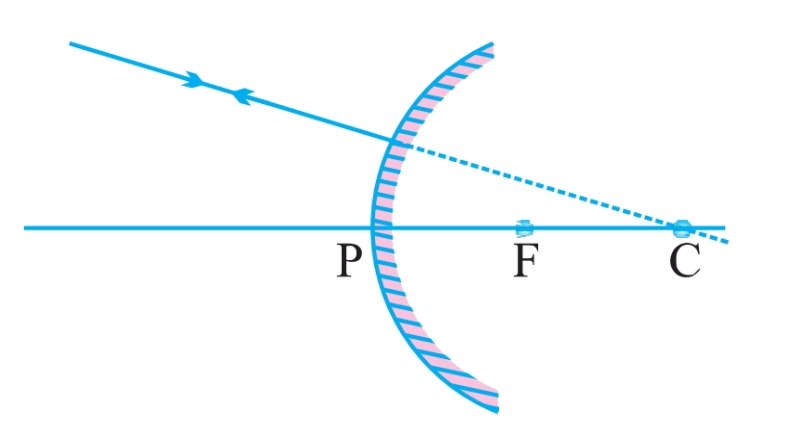
मुख्य अक्ष से तिरछी किरणें (Oblique Rays):
- तिरछी किरणें परावर्तित होकर तिरछी दिशा में निकलती हैं, और आपतन बिंदु पर इनका परावर्तन मुख्य अक्ष के समान कोण पर होता है।

| बिंब की सिथति |
प्रतिबिंब की स्थिति |
प्रतिबिंब का आकार |
प्रतिबिंब की प्रकृति |
| अनन्त पर |
फोकस पर दर्पण
के पीछे
|
अत्याधिक छोटा
बिंदु के आकार का
|
आभासी तथा सीधा |
| अनन्त तथा दर्पण के ध्रुव P के बीच |
P तथा F के बीच
दर्पण के पीछे
|
दर्पण के पीछे
छोटा
|
आभासी तथा सीधा |
किरण आरेख
1. अनन्त पर

2. अनन्त तथा दर्पण के ध्रुव P के बीच

उत्तल दर्पणों के उपयोग
1.वाहनों में उत्तल दर्पण:
- ड्राइवर को पीछे के वाहनों को देखने के लिए उपयोग।
- हमेशा सीधा और छोटा प्रतिबिंब बनाते हैं।
- बड़े क्षेत्र को देखने में मदद करते हैं।
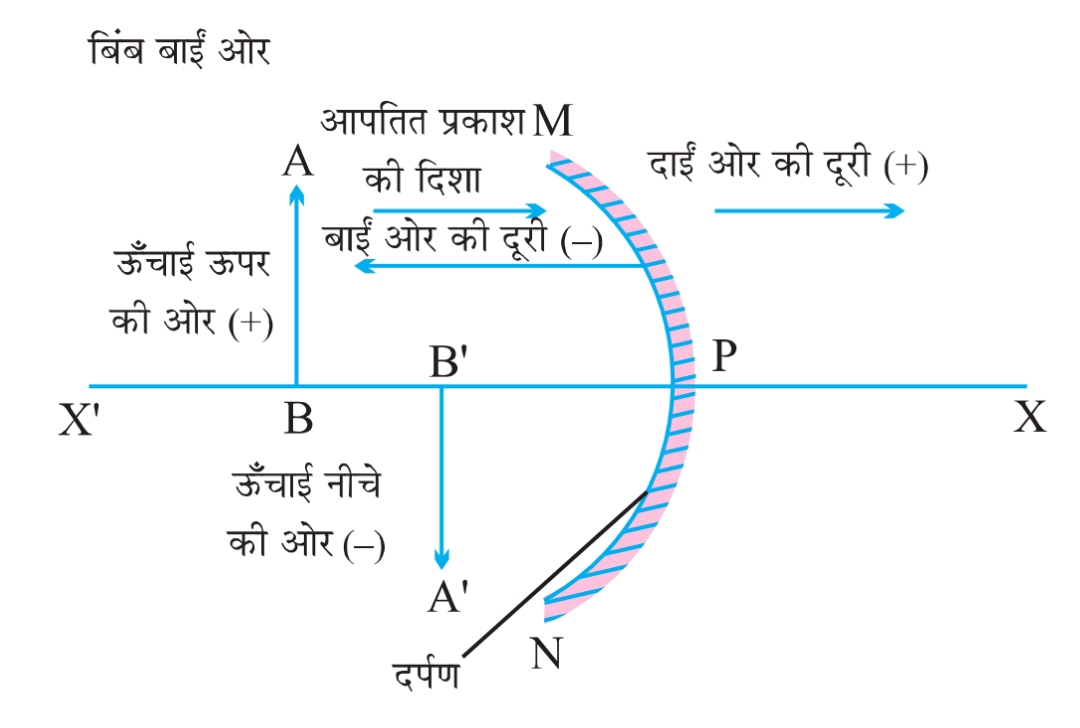
गोलीय दर्पणों द्वारा परावर्तन के लिए चिन्ह परिपाटी (Sign Convention):
1.बिंब का स्थान:
- बिंब हमेशा दर्पण के बाईं ओर होता है, यानी बिंब से प्रकाश बाईं ओर से आपतित होता है। (बिंब की दूरी ऋणात्मक होती है)
2.दूरी मापने का तरीका:
- सभी दूरियाँ दर्पण के ध्रुव से मापी जाती हैं, मुख्य अक्ष के समांतर।
3.धनात्मक और ऋणात्मक दिशाएँ:
- दाईं ओर (+x अक्ष) मापी गई दूरियाँ धनात्मक होती हैं।
- बाईं ओर (-x अक्ष) मापी गई दूरियाँ ऋणात्मक होती हैं।
- ऊपर (+y अक्ष) की दूरियाँ धनात्मक होती हैं।
- नीचे (-y अक्ष) की दूरियाँ ऋणात्मक होती हैं।
4.बिंब की दूरी (u):
- बिंब की दूरी हमेशा ऋणात्मक होती है।
5.फोकस की दूरी (f):
- अवतल दर्पण की फोकस दूरी ऋणात्मक होती है।
- उत्तल दर्पण की फोकस दूरी धनात्मक होती है।
दर्पण सूत्र और आवर्धन (Mirror Formula and Magnification):
दर्पण सूत्र (Mirror Formula):
1/f = 1/v + 1/u
- v = प्रतिबिंब की दूरी (image distance)
- u = वस्तु की दूरी (object distance)
- f = फोकस दूरी (focal length
आवर्धन (Magnification):
- आवर्धन m वह अनुपात है, जो यह बताता है कि प्रतिबिंब वस्तु के आकार से कितना बड़ा या छोटा है। इसे प्रतिबिंब की ऊँचाई h' और वस्तु की ऊँचाई h के अनुपात के रूप में व्यक्त किया जाता है: m = h′/h = -v/u
-
- m = आवर्धन (Magnification)
- h' = प्रतिबिंब की ऊँचाई (image height)
- h = वस्तु की ऊँचाई (object height)
आवर्धन के गुण:
- यदि m ऋणात्मक है, तो प्रतिबिंब वास्तविक होता है।
- यदि m धनात्मक है, तो प्रतिबिंब आभासी होता है।
- यदि m = 1, तो प्रतिबिंब का आकार वस्तु के आकार के बराबर होता है।
- यदि m > 1, तो प्रतिबिंब वस्तु से बड़ा होता है।
- यदि m < 1, तो प्रतिबिंब वस्तु से छोटा होता है।
समतल दर्पण (Plane Mirror):
समतल दर्पण का आवर्धन हमेशा m = +1 होता है।
यह संकेत करता है कि प्रतिबिंब का आकार वस्तु के आकार के बराबर होता है और यह आभासी (virtual) होता है।
दर्पण प्रकार के अनुसार आवर्धन:
- यदि m = +ve और m < 1, तो दर्पण उत्तल (Convex) है।
- यदि m = +ve और m > 1, तो दर्पण अवतल (Concave) है।
- यदि m = -ve, तो दर्पण अवतल (Concave) है।
- m=1 and h′ = h ⇒ प्रतिबिंब और वस्तु का आकार समान।
- m<1 and h′ < h ⇒ प्रतिबिंब वस्तु से छोटा।
- m>1 and h′ > h ⇒ प्रतिबिंब वस्तु से बड़ा।
प्रकाश का अपवर्तन (Refraction of Light)
जब प्रकाश एक माध्यम से दूसरे माध्यम में तिरछा होकर प्रवेश करता है, तो उसकी दिशा बदल जाती है। इसे प्रकाश-अपवर्तन कहते हैं।
प्रकाश-अपवर्तन के उदाहरण:
- स्विमिंग पूल: अपवर्तन के कारण स्विमिंग पूल का तल वास्तविक स्थिति से विस्थापित हो जाता है।
- पानी में डूबी पेंसिल: पानी में डूबी पेंसिल वायु और पानी के बीच के पृष्ठ पर टेढ़ी दिखती है।
- काँच में नीबू: काँच के गिलास में नीबू वास्तविक आकार से बड़ा प्रतीत होता है।
- कागज पर लिखे शब्द: गिलास स्लैब से देखने पर कागज पर लिखे शब्द ऊपर उठे हुए दिखाई देते हैं।
काँच की आयताकार स्लैब से अपवर्तन:
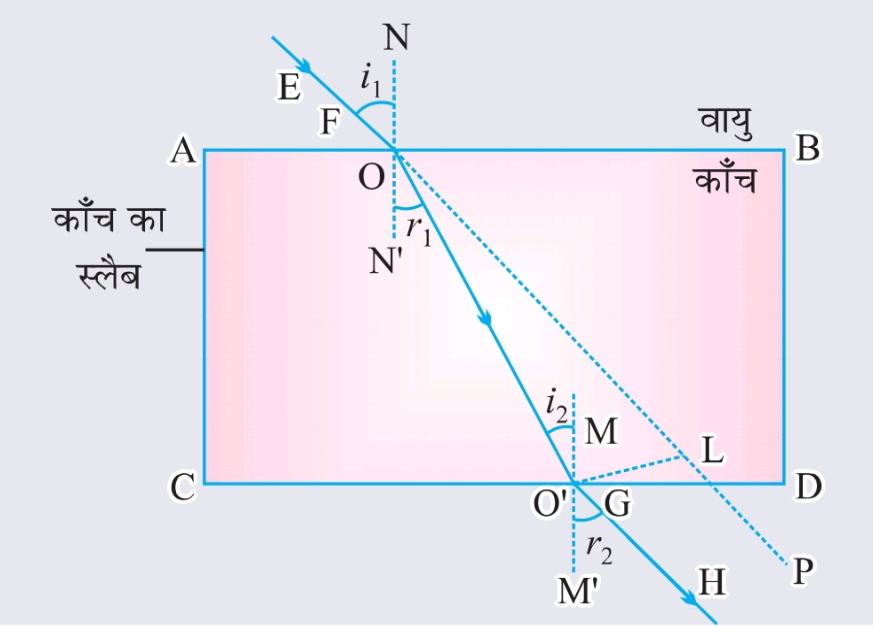
जब प्रकाश काँच की स्लैब से होकर गुजरता है, तो उसकी दिशा बदल जाती है।
प्रकाश-अपवर्तन के नियम (Laws of Refraction):
1. पहला नियम: आपतित किरण, अपवर्तित किरण , अभिलंब और दोनों माध्यमों को पृथक करने वाला पृष्ठ आपतन बिंदु पर एक ही तल में होते हैं।
2. दूसरा नियम (स्नेल का नियम):
n1: पहले माध्यम का अपवर्तनांक।
n2: दूसरे माध्यम का अपवर्तनांक।
स्नेल का नियम : आपतन कोण (i) और अपवर्तन कोण (r) के साइन (sine) का अनुपात स्थिर होता है, जो दोनों माध्यमों के अपवर्तनांक (refractive index) के अनुपात के बराबर होता है।
sini/sinr = n2/n1
अपवर्तनांक (Refractive Index):
- माध्यम 1 के सापेक्ष माध्यम 2 का अपवर्तनांक n12 द्वारा व्यक्त किया जाता है।
- निर्वात के सापेक्ष अपवर्तनांक: जब माध्यम निर्वात या वायु होता है, तो माध्यम 2 का अपवर्तनांक निर्वात के सापेक्ष माना जाता है, जिसे निर्वात अपवर्तनांक कहते हैं।उदाहरण : हीरा का अपवर्तनांक सबसे अधिक 2.42 है। इसका मतलब है कि प्रकाश की गति हीरे में निर्वात की तुलना में 1/2.42 गुना धीमी होती है।
प्रकाशिक सघन और विरल माध्यम:
- एक ऐसा माध्यम जिसका अपवर्तनांक अधिक हो, उसे प्रकाशिक सघन कहा जाता है
- एक ऐसा माध्यम जिसका अपवर्तनांक कम हो, उसे प्रकाशिक विरल कहा जाता है।

अपवर्तन (Refraction):
जब प्रकाश किरण एक विरल माध्यम (जैसे वायु) से एक सघन माध्यम (जैसे पानी या कांच) में जाती है, तो उसकी गति धीमी हो जाती है और प्रकाश की किरण अभिलंब की ओर झुक जाती है (अभिलंब वह रेखा है जो सतह के प्रति लंबवत होती है)।
गोलीय लेंस:
दो तलों से घिरा हुआ कोई पारदर्शी माध्यम जिसका एक या दोनों तल गोलीय है, लेंस कहलाता है।
लेंस के प्रकार:
उत्तल लेंस (Convex Lens):
- यह बीच में मोटा और किनारों पर पतला होता है।
- इसे अभिसारी लेंस (Converging Lens) भी कहते हैं क्योंकि यह प्रकाश किरणों को केंद्र की ओर अभिसरित करता है।
अवतल लेंस (Concave Lens):
- यह किनारों पर मोटा और बीच में पतला होता है।
- इसे अपसारी लेंस (Diverging Lens) कहा जाता है क्योंकि यह प्रकाश किरणों को बाहर की ओर अपसारित करता है।
उत्तल लेंस के किरण आरेख नियम:
-
मुख्य अक्ष के समांतर आने वाली कोई भी प्रकाश किरण उत्तल लेंस से गुजरने के बाद दूसरी ओर के मुख्य फोकस से गुजरती है।
-
मुख्य फोकस से होकर आने वाली कोई प्रकाश किरण लेंस से अपवर्तन के बाद मुख्य अक्ष के समांतर हो जाती है।
-
लेंस के प्रकाशिक केंद्र से होकर गुजरने वाली किरण बिना किसी विचलन के गुजरती है।
उत्तल लेंस द्वारा बनने वाले प्रतिबिंब की स्थितियां:
|
क्रम
|
बिंब की स्थिति
|
प्रतिबिंब की स्थिति
|
प्रतिबिंब का आकार
|
प्रकृति
|
|
1
|
अनंत पर
|
F₂ पर
|
अत्यधिक छोटा
|
वास्तविक और उल्टा
|
|
2
|
2F₁ से परे
|
F₂ और 2F₂ के बीच
|
छोटा
|
वास्तविक और उल्टा
|
|
3
|
2F₁ पर
|
2F₂ पर
|
समान आकार
|
वास्तविक और उल्टा
|
|
4
|
F₁ और 2F₁ के बीच
|
2F₂ के पार
|
बड़ा
|
वास्तविक और उल्टा
|
|
5
|
F₁ पर
|
अनंत पर
|
अत्यधिक बड़ा
|
वास्तविक और उल्टा
|
|
6
|
F₁ और O के बीच
|
उसी ओर
|
बड़ा
|
आभासी और सीधा
|
उत्तल लेंस के किरण आरेख :
1. अनंत पर

2. 2F₁ से परे
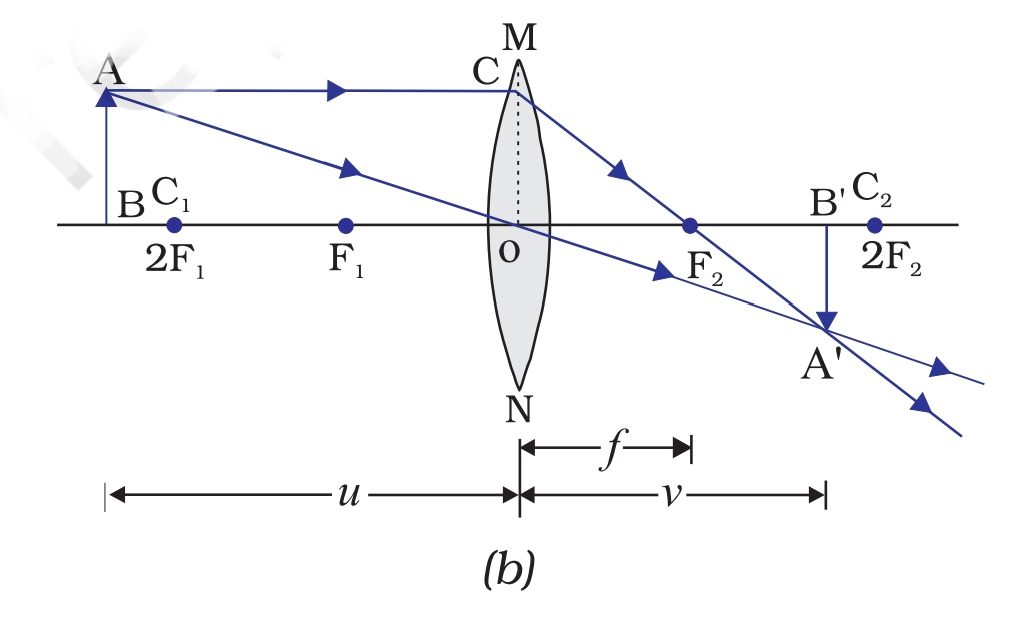
3. 2F₁ पर
4. F₁ और 2F₁ के बीच

5. F₁ पर

6. F₁ और O के बीच
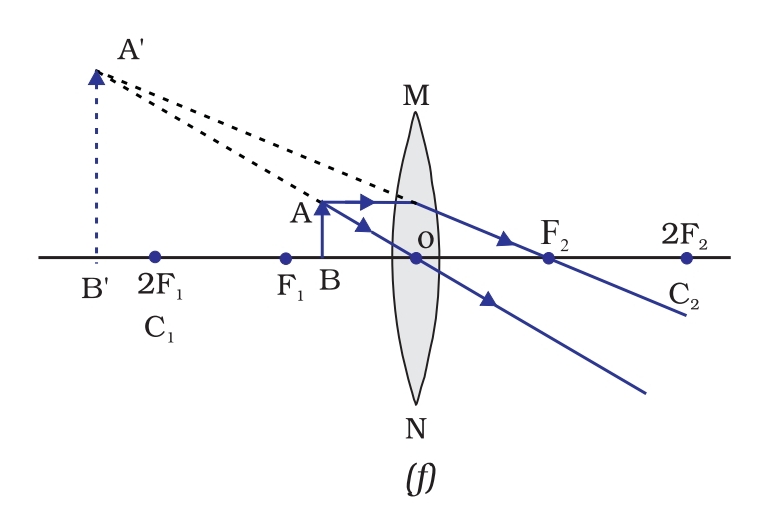
अवतल लेंस के किरण आरेख नियम:
- मुख्य अक्ष के समांतर आने वाली कोई किरण अपवर्तन के बाद लेंस के उसी ओर मुख्य फोकस से होकर गुजरती प्रतीत होती है।
- मुख्य फोकस से होकर आने वाली कोई किरण अपवर्तन के बाद मुख्य अक्ष के समांतर हो जाती है।
- प्रकाशिक केंद्र से होकर गुजरने वाली कोई किरण बिना विचलन के गुजरती है।
अवतल लेंस द्वारा बनने वाले प्रतिबिंब की स्थितियां:
|
क्रम
|
बिंब की स्थिति
|
प्रतिबिंब की स्थिति
|
प्रतिबिंब का आकार
|
प्रकृति
|
|
1
|
अनंत पर
|
F₁ पर
|
अत्यधिक छोटा
|
आभासी और सीधा
|
|
2
|
अनंत और O के बीच
|
F₁ और O के बीच
|
छोटा
|
आभासी और सीधा
|
अवतल लेंस के किरण आरेख
1. अनंत पर 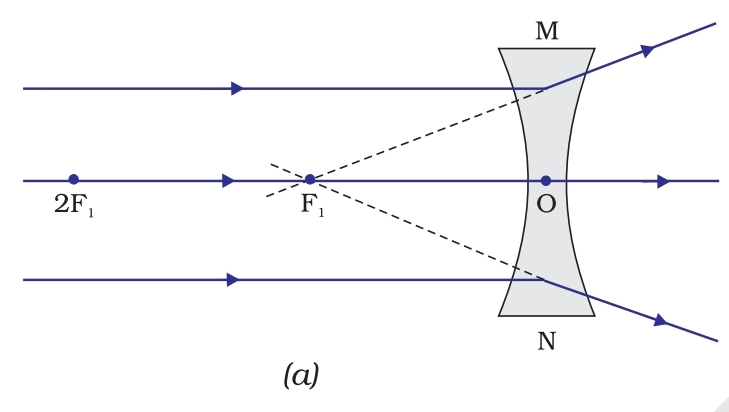
2. अनंत और O के बीच 
लेंस के लिए चिन्ह परिपाटी (Sign Convention):
- उत्तल लेंस की फोकस दूरी धनात्मक होती है।
- अवतल लेंस की फोकस दूरी ऋणात्मक होती है।
लेंस सूत्र:
1/f = 1/v - 1/u
जहाँ,
- f = फोकस दूरी
- v = प्रतिबिंब की दूरी
- u = बिंब की दूरी
आवर्धन (Magnification):
आवर्धन दर्शाता है कि बिंब की ऊँचाई के सापेक्ष प्रतिबिंब कितना बड़ा या छोटा है।
m = h′/h = v/u
जहाँ,
- m = आवर्धन
- h' = प्रतिबिंब की ऊँचाई
- h = बिंब की ऊँचाई
लेंस की क्षमता (Power of Lens):
- किसी लेंस द्वारा किरणों को अपसारित या अभिसारित करने की क्षमता उसकी क्षमता (Power) कहलाती है।
- लेंस की क्षमता, उसकी फोकस दूरी का व्युत्क्रम होती है: P = 1/f
- इसका मात्रक डायॉप्टर (Diopter, D) होता है।
- उत्तल लेंस की क्षमता धनात्मक होती है, जबकि अवतल लेंस की क्षमता ऋणात्मक होती है।
लेंसों का संयोजन:
- जब कई लेंस एक साथ रखे जाते हैं, तो उनकी कुल क्षमता का योग किया जाता है: P = P1 + P2 + P3 +...
- इससे प्रतिबिंब अधिक आवर्धित और स्पष्ट बनता है।
































