Light – Reflection and Refraction
What is Light?
Light is a form of energy that enables us to see objects.
Properties of Light
Laws of Reflection
Image Formation
An image is formed at the point where two or more reflected rays actually meet or appear to meet.
Types of Images
| Real Image | Virtual Image |
| (i) Formed when reflected rays actually intersect. | (i) Formed when reflected rays appear to intersect. |
| (ii) Can be obtained on a screen. | (ii) Cannot be obtained on a screen. |
| (iii) Always inverted. | (iii) Always erect (upright). |
Image Formed by a Plane Mirror
Lateral Inversion
In lateral inversion, the right side of the object appears as the left side and vice versa.
Spherical Mirrors
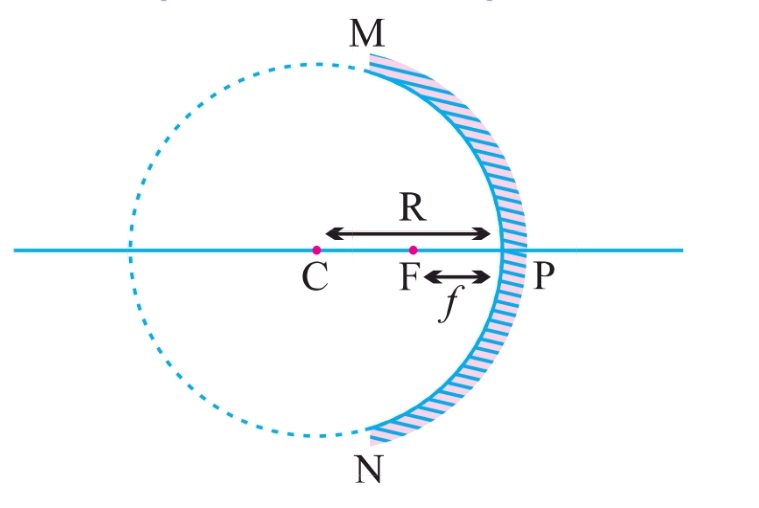
Important Terms Related to Spherical Mirrors
1. Pole (P):
2. Principal Axis:
3. Centre of Curvature (C):
4. Radius of Curvature (R):
5. Aperture (MN):
6. Principal Focus (F):
7. Focal Length (f):
Important Relation
Concave Mirror
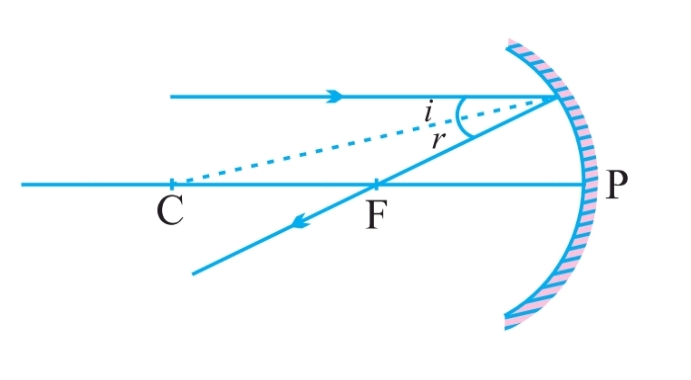
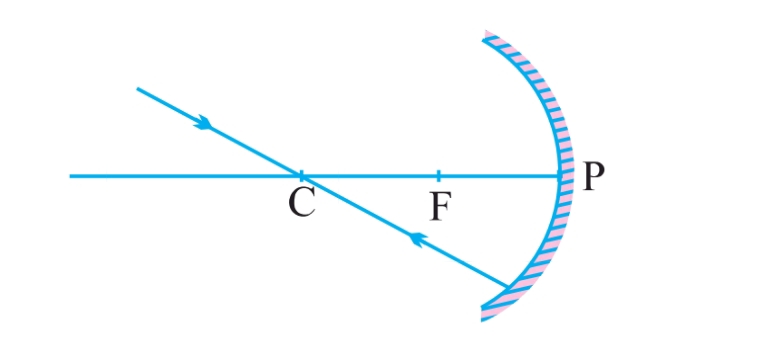
Rules for Ray Diagrams


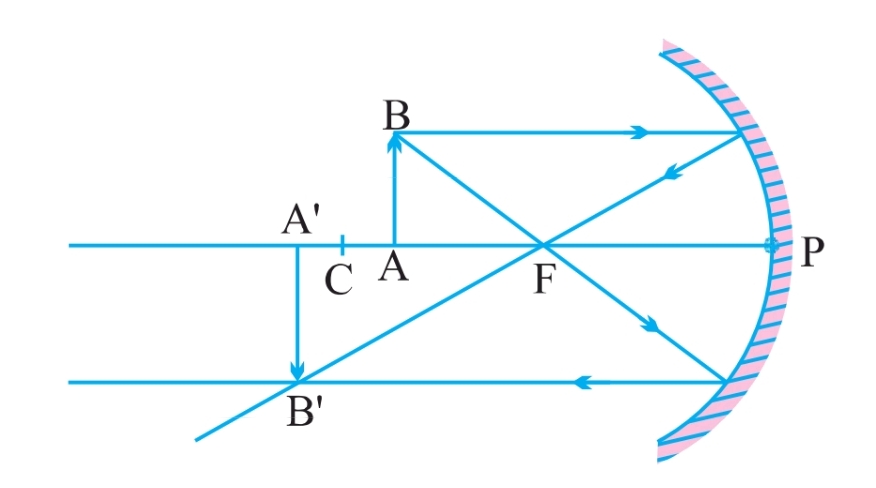
| Position of Object | Position of Image | Size of Image | Nature of Image |
|---|---|---|---|
| At infinity | At focus | Highly diminished | Real and inverted |
| Beyond C | Between F and C | Diminished | Real and inverted |
| At C | At C | Same size | Real and inverted |
| Between C and F | Beyond C | Enlarged | Real and inverted |
| At F | At infinity | Highly enlarged | Real and inverted |
| Between P and F | Behind the mirror | Enlarged | Virtual and erect |
( 1 ). At infinity

( 2 ). Beyond C

( 3 ). At C

( 4 ). Between C and F
( 5 ). At F

( 6 ). Between P and F
Uses of Concave Mirrors
Convex Mirror
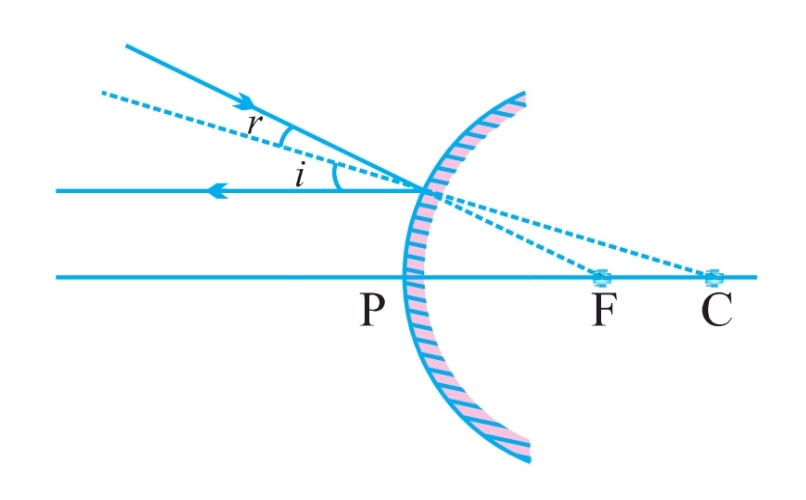
Parallel Ray (Ray Parallel to Principal Axis):
When a ray of light travels parallel to the principal axis towards the mirror, the reflected ray appears to pass through the principal focus (F).
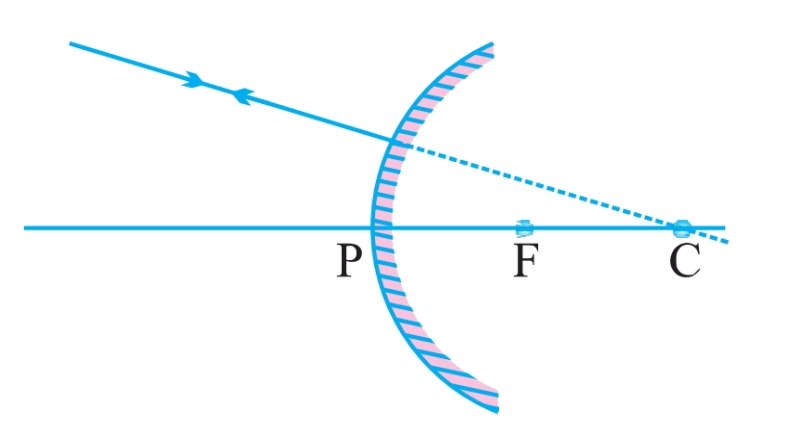
Ray from the Center of Curvature:
If a ray of light passes through the center of curvature (C), it reflects back along the same path, as it strikes the mirror at 90° (normal incidence).
Oblique Rays:
Oblique rays are reflected obliquely, making equal angles with the principal axis at the point of incidence.

| Object Position | Image Position | Image Size | Nature of Image |
|---|---|---|---|
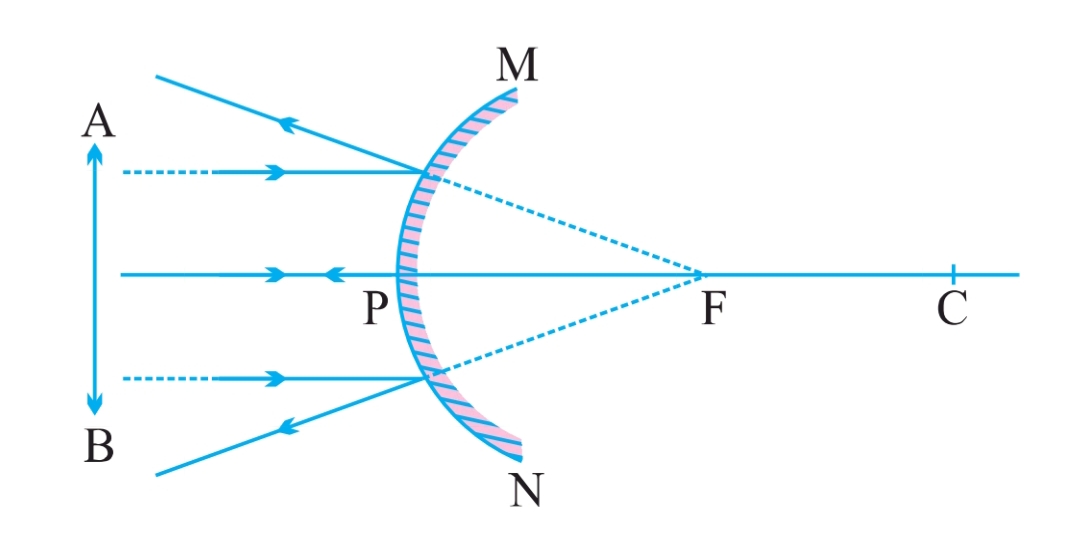
| At infinity | Behind the mirror at the focus (F) | Very small, point-sized | Virtual and erect |
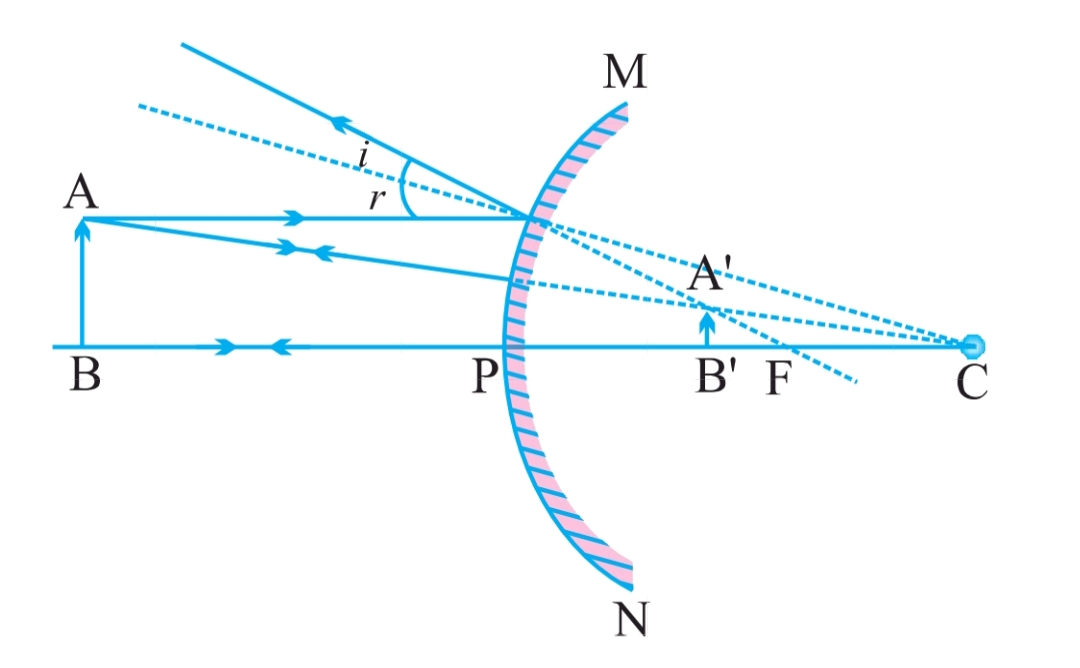
| Between infinity and pole (P) | Between pole (P) and focus (F) behind the mirror | Small | Virtual and erect |
Ray Diagrams
1. At Infinity
2. Between Infinity and Pole (P)
Uses of Convex Mirrors
1. In Vehicles:
Sign Convention for Reflection by Spherical Mirrors
1. Position of Image:
2. Measurement of Distances:
3. Positive and Negative Directions:
4. Object Distance (u):
5. Focal Length (f):
Mirror Formula and Magnification
Mirror Formula:
1/f = 1/v + 1/u
Where:
Magnification (m):
Magnification (m) is the ratio of the height of the image (h′) to the height of the object (h).
m = h′/h = -v/u
Where:
mm = magnification
h′h′ = height of the image
hh = height of the object
Properties of Magnification:
If mm is negative, the image is real.
If mm is positive, the image is virtual.
If m=1m = 1, the image size equals the object size.
If m>1m > 1, the image is larger than the object.
If m<1m < 1, the image is smaller than the object.
For a plane mirror, magnification m=+1m = +1.
This means the image is virtual, erect, and equal in size to the object.
If m=+vem = +ve and m<1m < 1: Mirror is Convex.
If m=+vem = +ve and m>1m > 1: Mirror is Concave.
If m=−vem = -ve: Mirror is Concave.
m=1m = 1 and h′=hh′ = h: Image and object are of same size.
m<1m < 1 and h′<hh′ < h: Image is smaller than the object.
m>1m > 1 and h′>hh′ > h: Image is larger than the object.
When light passes obliquely from one medium to another, its direction changes. This phenomenon is called refraction of light.
Swimming Pool: The bottom appears raised due to refraction.
Pencil in Water: A pencil partly immersed in water appears bent at the surface.
Lemon in Glass: A lemon in a glass of water looks magnified.
Text under Glass Slab: Words appear raised when viewed through a glass slab.
When light passes through a rectangular glass slab, it bends twice and emerges parallel to the incident ray but displaced sideways.
First Law:
The incident ray, the refracted ray, and the normal at the point of incidence all lie in the same plane.
Second Law (Snell’s Law):
where,
n1: Refractive index of the first medium
n2: Refractive index of the second medium
The refractive index of medium 2 with respect to medium 1 is denoted as n21n_{21}.
When the first medium is air or vacuum, the index is called absolute refractive index.
Example: The refractive index of diamond is 2.42, meaning light travels 2.42 times slower in diamond than in vacuum.
A medium with higher refractive index → Optically Denser.
A medium with lower refractive index → Optically Rarer.
When light travels from a rarer to a denser medium (e.g., air to glass), it slows down and bends towards the normal.
A lens is a transparent medium bounded by two surfaces, at least one of which is spherical
1. Convex Lens (Converging Lens):
Thicker in the middle and thinner at the edges.
Converges light rays to a point.
2. Concave Lens (Diverging Lens):
Thinner in the middle and thicker at the edges.
Diverges light rays outward.
A ray parallel to the principal axis passes through the focus after refraction.
A ray passing through the focus emerges parallel to the principal axis.
A ray through the optical center passes without deviation.
| No. | Object Position | Image Position | Image Size | Nature |
|---|---|---|---|---|
| 1 | At infinity | At F₂ | Highly diminished | Real and inverted |
| 2 | Beyond 2F₁ | Between F₂ and 2F₂ | Smaller | Real and inverted |
| 3 | At 2F₁ | At 2F₂ | Same size | Real and inverted |
| 4 | Between F₁ and 2F₁ | Beyond 2F₂ | Enlarged | Real and inverted |
| 5 | At F₁ | At infinity | Highly enlarged | Real and inverted |
| 6 | Between F₁ and O | On the same side | Enlarged | Virtual and erect |
At infinity
Beyond 2F₁
At 2F₁
Between F₁ and 2F₁
At F₁
Between F₁ and O
A ray parallel to the principal axis appears to diverge from the focus (F₁).
A ray directed towards the focus emerges parallel to the principal axis.
A ray through the optical center passes undeviated.
| No. | Object Position | Image Position | Image Size | Nature |
|---|---|---|---|---|
| 1 | At infinity | At F₁ | Highly diminished | Virtual and erect |
| 2 | Between infinity and O | Between F₁ and O | Diminished | Virtual and erect |
Focal length of convex lens → positive.
Focal length of concave lens → negative.





